Realtime contents based blog recommand system
이 글은 2015년 중앙대학교 Big Data 경진대회에 출품했던 프로젝트를 다시 재구성한 것입니다. 학생 프로젝트로 진행했던것이고, 해당 대회 금상을 받았습니다. 이 글에서는 최신 트렌드를 반영하지 않으며, 방구석에 있던 발표 자료를 보고 다시 작성하는 것입니다. 이 글에서 소개하는 아이디어는 저와 함께한 해당 프로젝트 팀원의 것이며, 마음대로 차용하지 않으셨으면 합니다. 이 글에서는 “현재” 라고 언급되는 것이 2015년 3분기임을 감안하시고 읽어주시면 감사 하겠습니다. 고작 2년사이에, 딥러닝이 세상을 지배하고 있어서, 이런 아이디어는 더 이상 useful 하지 않을수도 있습니다.
문제 설정
블로그 글은 많은데, 이 글과 비슷한 주제의 글은?
수많은 블로그 글들이 난립하지만, 비슷한 주제의 글을 찾기란 하늘의 별따기 보다 어렵습니다. 그런 것은 대형블로그 운영사도 마찬가지 인듯 합니다. 주제별 글을 볼수 있는 란이 있지만, 아직까지는 카테고리나 tag에 기반한 추천을 사용하는 것 같습니다.
네이버 블로그는 아직까지 카테고리 기반이고, 다음블로그도 카테고리 기반, 이글루스 벨리도 카테고리 기반입니다. 올블로그가 조금 특이하게 메타 블로그 추천수 기반입니다. 비슷한 주제의 글을 찾는 일이 얼마나 어려운 일이길래 수년간의 노하우가 쌓인 블로그들도 빅데이터 분석 기반 추천을 시도하지 않는 것처럼 보입니다. 백엔드 알고리즘은 또 다른 무엇이 있는지도 모르겠지만은요.
그래서 시도할 것은 “비슷한 주제의 블로그를 찾는 시스템 만들기”입니다.
문제 분석
우선 문제 분석 부터 해야 합니다. 비슷한 주제는 어떻게 컴퓨터가 알아들을 수 있게 정의하고, 어떤 종류의 추천 시스템을 선택해야 하는지 결정해야 합니다.
추천 시스템의 종류
추천 시스템을 만들려면 추천 시스템에는 어떤것이 있는지 알아야지요. 추천 시스템은 크게 다음과 같이 분류할수 있습니다.
- contents based
- 아이템 자체의 특성을 활용하여 추천하는 방법
- collaborative based
- 사용자의 행동 방식을 기반으로 아이템을 추천하는 방법
- item based
- 아이템과 아이템 사이의 유사도 산출을 사용한 방법
- user based
- 사용자와 사용자 사이의 유사도 산출을 사용한 방법
contents based recommend system은 간단합니다. content의 특성을 이용해서 유사한 content를 찾아 내는 것입니다. content의 특성이 어떤지 알아야 유사한 content를 찾아 낼수 있고, content가 유사하다는 것이 어떤 것인지 잘 정의 할수 있어야 제대로 된 추천이 가능합니다. 비슷한 단어를 가지고 있는 글을 추천한다던지, 비슷한 색감을 가진 사진을 추천하는 것들이 바로 content based recommend system 입니다.
반면 collaborative base recommendation system은 조금 더 복잡합니다. 사용자의 클릭 빈도와 같은 content 외적인 요소를 가지고 유사성을 찾아 냅니다.
item based는 이 아이템과 같이 선택된 아이템을 기억해 뒀다가 다른 사용자가 둘중 하나를 선택하면 다른 하나를 추천하는 방식입니다. 쇼핑몰에서 보는 “같이 구매한 상품” 이 여기에 해당됩니다. 마트에 가면 가끔 스테이크용 고기 매대 앞에 스테이크 소스 매대가 있는데 이도 유사한 것입니다.
user based는 여기서 한단계 더 나아간 것입니다. 같이 선택한 아이템이 아니라 비슷한 선택을 한 사용자를 찾은 후 그 사용자가 선택한 다른 아이템을 추천합니다. “20대가 많이 고른 물품” 과 같이 특정 사용자를 그룹화 하고 그 선택을 따라 합니다.
collaborative base recommendation system은 훨씬 더 유연하고 사람의 사고에 맞는 추천을 할수 있습니다. 하지만 사용자가 적거나 해당 데이터를 모을수가 없는 상황에서는 추천이 불가능 합니다. 심지어 해당 데이터을 되도록 많이 모아야 하는데, 그러기가 쉽지 않다는 문제점도 있습니다.
우리는 구글도 아니고 블로그 플랫폼을 운영하고 있지도 않으므로 어떤 사용자가 어떤 글을 보았는지 알수가 없습니다. 따라서 다른 방법은 제쳐두고 아쉽지만 그래도 시도할수 있는 유일한 방법인 contents based로 진행하기로 합시다.
비슷한 글?
content기반으로 분석하기로 마음 먹었으므로 어떤 content가 비슷한 content 일지 컴퓨터가 알아먹도록 정의 해 보도록 합시다. 사람이야 글을 읽으면 비슷하다는 것을 금방알수 있지만 컴퓨터에게는 쉽지 않은 일입니다.
TF-IDF
여러가지 고급 기법들이 있을수 있겠지만 쉽게 쉽게 가기 위해 일단 디테일은 제쳐두고 다음을 고려해 봅시다.
어떤 글이 비슷하다는 것은 “비슷한 구문이 등장” 하거나 “비슷한 단어가 등장” 하는 것이라고 생각할수 있습니다. 특히 같은 구문이 등장한다면 “인용” 이거나 “표절” 이겠죠. 둘다 비슷한 주제를 다루고 있다는 강력한 증거가 될수 있습니다. 하지만, 비슷한 구문을 찾아 내기란 쉬운 문제가 아닙니다. 한국어의 특성상 조사가 종종 달라지거나 띄워쓰기가 틀려지곤 하는데, 컴퓨터는 이를 인식할수 없기 때문이죠. 비슷한 단어는 어떨까요. 단지 단어가 등장하는 것만으로는 비슷하다고 할수 없죠. 우연이 그 단어가 쓰일수도 있으니까요. 하지만 중요한 단어가 비슷한 빈도로 등장하면 어떨까요? 그렇다면 비슷한 주제의 글이라고 볼수 있지 않을까요?
다행이 똑똑한 사람들이 중요한 단어를 찾는 수식을 만들어 두었습니다. TF-IDF 가 그것이죠.
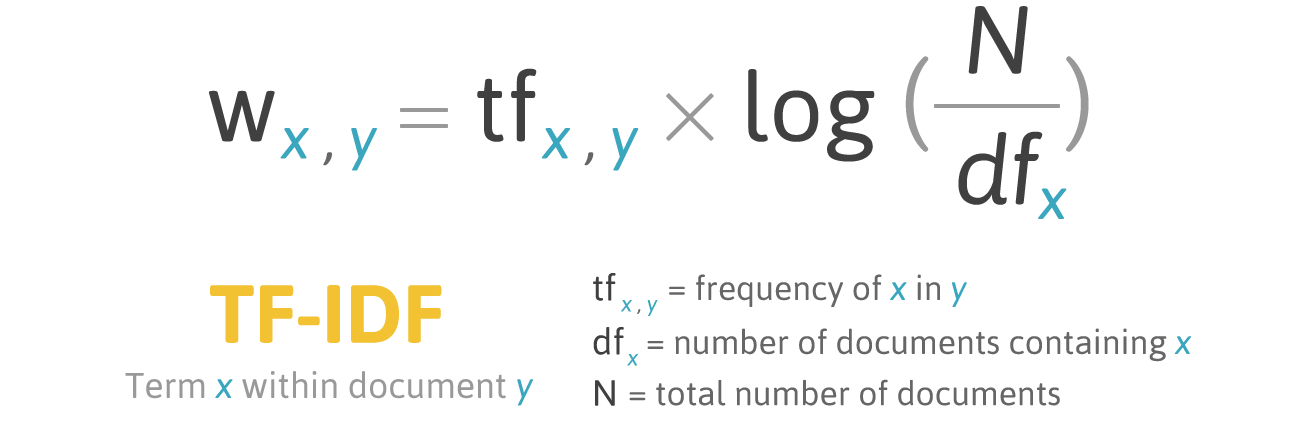
- TF(Term Frequency) : 문서에서 각 단어가 등장한 빈도를 나타낸다.
- DF(Document Frequency) : 모든 문서에서 해당 단어가 등장한 문서의 수를 나타낸다.
- TF-IDF : DF의 역수와 TF의 곱을 통해 얻는 값으로, 모든 문서에 대해서 단어가 어느 정도로 중요한 지를 나타내는 지표이다.
TF-IDF는 한 문서에서 그 단어가 얼마나 중요한 단어인지 나타내는 지표입니다. TF-IDF는 그 문서에서 자주 쓰이면 쓰일수록 수치가 높게 나타납니다. 쉽게 말해 한 글에서의 단어의 등장빈도와 결과 값이 정비례 합니다. 반면 다른 문서에 등장 하면 등장할수록 수치가 낮게 나타납니다. 다른문서에 등장한 빈도와 반비례 하는 것이지요. 즉 “물리학”, “운영체제”, “시분할시스템” 과 같은 특이한 단어들은 점수가 높게 되고, “나”, “우리” 와 같이 흔한 단어는 점수가 낮아 집니다. 보통 단어의 분포는 log 분포1를 보이기에 log 함수를 이용해 normalize 합니다. 즉 단어별 TF-IDF의 값이 유사하다면 두 글은 비슷한 주제의 글이라고 볼수 있습니다.
유사도
그렇다면 두 값이 유사하다는 것은 어떤 의미일까요. TF-IDF는 단어별로 값이 뽑히기 때문에 단순히 몇몇 단어의 값이 유사하다고 해서 두 글이 유사하다고 할수 없습니다. 너무도 많은 변수가 있기 떄문이지요. 다음과 같은 케이스를 고려해 봅시다.
- A글 TF-IDF
- 설탕: 1.0
- 냄비 : 0.3
- 가열 : 0.1
- B글 TF-IDF
- 설탕: 1.1
- 솜사탕: 0.5
- C글 TF-IDF
- 설탕: 0.5
- 냄비: 0.1
- 냉장고: 0.1
- 불: 0.1
- 그릇: 0.1
B와 C중 A글과 비슷한 글은 무엇일까요? 수치만 보고는 쉽사리 답을 하기 어렵습니다. 따라서 우리는 여러개의 key-value 쌍을 갖는 두 그룹 사이의 유사도를 수학적으로 정의할 필요가 있습니다. 수학적으로 정의 된다면 계산은 컴퓨터에게 맡기면 되니까요. big data 처리에서는 흔히 두가지의 유사도가 자주 사용됩니다. jaccard 유사도와 cosine 유사도이죠.
Jaccard 유사도는 두 그룹에서 같은 key가 등장하기만 하면 +1을 합니다. 같은 key가 많으면 유사도가 높은거죠. Cosine 유사도는 벡터와 consine의 수학적 특성을 이용하는데 각각의 key를 하나의 축으로 보고 value를 대응하여 vector를 그립니다. 두 vector 간의 cosine 값이 크면 유사도가 큰값이 됩니다. 이는 내적을 통해 쉽게 계산할수 있습니다.
Jaccard 는 각 key의 값이 중요치 않거나 key만 존재하는 경우에 사용 되고 consine은 각 value 도 중요할때에 사용됩니다. 여기서는 각 값도 중요하니 consine 유사도를 사용해야 겠네요.
소정리
정리하자면 비슷한 글이라는 것은 중요한 단어가 비슷한 빈도로 출현하는 것이고, 이는 TF-IDF로 수치적으로 나타낼수 있습니다. 이 TF-IDF가 서로 유사한 글은 비슷한 글인데 두 TF-IDF가 유사하다는 것은 consine 유사도를 사용하면 비슷한 정도를 수치적으로 나타낼수 있죠. 따라서 TF-IDF의 cosine 유사도가 높은 글이 비슷한 주제의 글이 되는 것입니다.
결국 처음에 풀고자 했던 “블로그 글은 많은데, 이 글과 비슷한 주제의 글은?“이라는 질문은 다음과 같이 수학적으로 재정의 될수 있습니다.
특정한 A글과 TF-IDF의 cosine 유사도가 높은 글을 찾는 문제
이제 문제를 나름 수학적으로 만들었으니 컴퓨터가 풀도록 만들면 되겠네요.
문제의 문제
그런데 뭔가 이상한 부분이 있습니다. 우선 cosine 유사도를 계산하려면 각 TF-IDF를 벡터로 나타내야 합니다. 그런데 블로그 글은 수천만개에 달합니다. 며칠간 크롤링으로 모은 블로그 글은 6000만개 입니다. 즉 6000만개의 백터를 서로 비교 해야 합니다. 더군다나 TF-IDF 의 벡터의 element 갯수는 한국어 단어의 갯수와 맞먹을텐데, 한국어 사전에 등록된 단어는 51만개 입니다. consine 유사도를 구하기 위해서는 내적을 해야 하는데 그렇게 되면 필요한 연산수는 단순히 계산해도 6000만 * 51만 이 됩니다. 즉 대략 30600000000000번 연산해야 합니다. 일반적인 연산 방법으로는 불가능 해보입니다2. 이래서야 실시간 시스템은 커녕 분단위의 연산으로도 부족해 보입니다.
이렇게 많은 연산을 해야 하는 근본적인 원인이 무엇일까요. 그것은 바로 데이터의 차원이 높기 때문입니다. TF-IDF는 단어별로 하나의 값을 가지기 때문에 51만 차원의 벡터로 나타내어 지는 것이지요. 대부분의 단어는 0개이지만, 어떤 단어가 등장할지 모르기 때문에 반드시 단어별로 하나의 차원을 가져야 합니다. 따라서 이 차원을 줄여야지 연산의 횟수를 줄일수 있습니다.
Local Sensitive Hashing
차원을 줄이는 여러가지 방법이 있지만, 기존 big data 처리 방법에서 자주쓰이는 방식으로는 LSH가 있습니다. LSH는 일종의 hash의 변형인데, 일반적인 hash 와는 달리 Diffuse 효과가 없습니다. 일반적인 hash 는 단 한 비트만 달라져도 결과값이 완전히 달라지는 효과가 있지만 LSH는 단 한비트가 달라지면 결과 값도 비슷 합니다. 따라서 보안적인 측면에서는 별 쓸모가 없지만, 비슷한것끼리 같이 묶어야 하는 경우에는 쓸모가 있죠. 일종의 차원 reduce 효과가 납니다. LSH 를 만족하는 해쉬 함수에는 MinHash, Random Hyperplane Projection 등이 있습니다. 유사도의 종류를 따라 써야하는 LSH함수도 달라집니다.
우리는 위에서 TF-IDF가 코사인 유사할때 같은 주제라고 판단하기로 하였으므로 코사인 유사도를 유지시켜주는 LSH를 써야 합니다.
Random Hyperplain
Random hyperplain은 hyperspace 상에 임의의 hyperplain을 두고 그 평면이 나눈 공간중 어디에 속하는 지를 체크하여 hash 함수로 사용합니다. 3차원 공간상에서 평면이 어느 사분면에 존재하는 지 따지는 것과 유사합니다. 코사인 유사도가 높을수록 공간상에 비슷한 위치에 있을 확률이 높으므로 평면으로 나누어진 half-hyperspace중에 같은 half-hyperspace에 속할 확률이 높아지는 원리입니다. 물론 충분한 갯수의 random hyperplain이 있어야 구분이 되겠지요. 많은 random hyperplain이 있을수록 각 블로그글들을 구분할수 있겠지만 연산하기는 점점더 어려울겁니다.
그럼 충분한 갯수의 random hyperplain은 몇개일까요?
그 수는 우리가 계산하기에는 충분하면서 동시에 하나하나의 블로그 글들은 구분할수 있어야 합니다. Random hyperplain에서 중요한것은 평면으로 나누어진 두개의 공간중 어디에 속하는가 입니다. 하나의 hyperplain에 대해서 단 두가지의 경우만 있는 것이지요. 우리는 이미 두가지의 경우만 가지고 있는 경우, 사용하기 좋은 표시 단위를 알고 있습니다. 1 bit 만으로 두가지의 경우를 나타낼수 있죠. 두 백터가 같은 공간의 속해있는지 아닌지 알기 위해서는 단지 두 bit를 XOR 하기만 하면 됩니다. 둘다 1이거나 둘다 0일경우 같은 공간이 있는 것이죠. 다행스럽게도 현대의 컴퓨터는 이 XOR연산을 어마어마한 빠르기로 할수 있습니다. 더군다나 아주 평범한 개인용 64bit 컴퓨터에서도 동시에 64개의 bit를 초당 수백만번 XOR 할수 도 있죠.
64개의 hyperplain으로 나누어 지는 공간의 갯수는 얼마일까요. 하나의 hyperplain은 2개의 공간을 만들고, 두개의 hyperplain은 2^2, 4개의 공간을 만듭니다. 64개의 hyperplain은 2^64개의 공간을 만들어 내죠. 이는 총 18446744073709551615개의 공간입니다. 1844경 6744조 737억 955만 1615개의 공간이죠. 6000만에 비해서는 어머어마하게 큰 숫자죠. 만약 TF-IDF의 벡터가 조금만 균등하게 분포한다고 하더라도 한 공간에는 거의 하나의 벡터만 포함될 정도의 숫자죠. 그러면서도 수백만분의 일초만에 계산이 가능합니다. 즉 64개정도의 random hyperplain을 사용하면 빠르게 계산이 가능 하면서도, 동시에 각 블로그를 구분하기에 충분한 random hyperplain의 갯수를 찾은것 같군요.
Random Hyperplain의 계산
특정 vector가 평면으로 나누어진 두 공간 중에 어디에 속하는지 계산하는 가장 간단한 방법은 백터의 내적입니다. 각 평면에는 그 평면을 특징짓는 법선 vector 가 있습니다. 이 법선 백터는 평면에 수직하게 뻗어 있죠. 따라서 평면으로 나누어진 두공간은 법선 벡터 방향과 그 반대 방향으로 나누어 집니다. 이 법선 벡터와 원래의 벡터가 이루는 각이 90도 이하라면 같은편에 90도 이상이라면 반대 편에 있는 것입니다. 여기서 벡터의 내적을 살펴보죠. 벡터의 내적은 두 벡터의 길이를 두 벡터사이의 코사인 값을 곱한것입니다. 그런데 이 코사인값은 90도 이하에서는 양수 이고 90도 이상에서는 음수 이죠. 따라서 법선 백터와 특정 벡터를 내적한 값이 음수라면 법선백터의 반대편에, 양수라면 같은 편에 있는 것입니다3.
- Zipf’s law
- 최근(2017년 3분기)의 GPGPU연산능력을 생각 하면 아예 불가능 하진 않아 보입니다.
1080 만세하지만, 이글에서 설명하는 테크닉은 GPGPU로도 계산할수 있기에 이 글에서 설명하는 테크닉과 GPGPU를 결합하면 무지막지한 성능을 내보일수 있을 것 같습니다. - 물론 평면이 원점을 지나야 하지만, 나중에 random plain을 만들면서 모두 원점을 지나도록 하면 됩니다.